Haryati , Haryati (2002) Analisis variansi multivariat dua faktor untuk rancangan faktorial dalam rancangan acak lengkapo model tetap. Undergraduate thesis, FMIPA UNDIP.
| PDF Restricted to Repository staff only 2523Kb | ||
| PDF 16Kb | |
| PDF 235Kb | |
| PDF 373Kb | |
| PDF 273Kb | |
| PDF 800Kb | |
| PDF Restricted to Repository staff only 1171Kb | ||
| PDF 208Kb | |
| PDF 215Kb | |
| PDF 362Kb |
Abstract
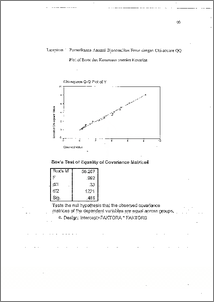
Analisis variansi rnultivariat dua faktor pada rancangan faktorial digunakan untuk menguji ada atau tidaknya perbedaan yang nyata tentang pengaruh masing-masing faktor dan interaksinya terhadap p respon (p > 1), atau menguji kesamaan vektor rata-rata dari beberapa populasi. Astrmsi yang diperlukan dalam hipotesis ini adalah Eijk berdistribusi E) yang diuji dengan plot quantil-quantil yang didekati dengan quantil chi-kuadrat dari (e,j, —) dengan x2(0 —1f2)/abn), S adalah matriks kovarian dari galat. Asinnsi kesamaan matriks kovarian dapat diuji dengan uji Box M. Hipotesis dapat diuji dengan statistik Wilk's A yang didekatkan ke distribusi F. Ho ditolak jika F > Ftabd atau P - value < CL Jika ada Ho yang ditolak berarti ada perbedaan vektor rata-rata perlakuan. Uji lanjut yang digunakan adalah kontras orthogonal multivariat . Hipotesis dapat diuji dengan statistik 1-lotelling's T2. Ho ditolak jika T2 T2„,p,„„(„_1) The two-factor of factorial design multivariate analysis of variance can be used for testing the significant difference the effect of each factors and its interaction to p observation (p > 1) or for testing equality mean vectors from several population. Assumption are required for this hypothesis are silk distribute as Np(0, E) can be test with plot quantiles are approached by chi-square quantiles from (eijk — — e) with x2((j — 1/2)/abn), S is covariance matrices of error. The assumption of equality of covariance matrices can be test with Bo's M tests. The hypothesizes can be tested with wilks'A statistics which approach to F distributions. Ho is rejected if F > Ftable or Pvalue < a. If there is Ho is rejected it means is difference of treatment mean vectors. Comparison of individual treatment mean vectors are requered multivariate orthogonal contrasts. Hypothesis can be test with Hotelling's T2 . Ho is rejected if T2 T2,z;p;:m(n-1).
| Item Type: | Thesis (Undergraduate) |
|---|---|
| Subjects: | Q Science > QA Mathematics |
| Divisions: | Faculty of Science and Mathematics > Department of Mathematics |
| ID Code: | 31738 |
| Deposited By: | Mr UPT Perpus 1 |
| Deposited On: | 24 Nov 2011 13:09 |
| Last Modified: | 24 Nov 2011 13:09 |
Repository Staff Only: item control page